MECANICA DEL FALLAMIENTO:TEORIA Y EXPERIMENTOS
CIRCULOS DE MOHR APLICADOS AL FALLAMIENTO
Los círculos de Mohr sirven para analizar las condiciones de stress necesarias para que se produzca
la ruptura sobre un determinado plano de fractura material (e.g. una falla) o bien sobre un plano de
fractura potencial.
Ecuaciones de los círculos de Mohr
Sea un cubo de roca en la Corteza terrestre ubicado a una cierta profundidad. Analícese el estado de
stress que actúa sobre un plano de fractura potencial P al interior del cubo, originado por la
aplicación de un stress, el cual es de tipo compresivo, esto es s1 = horizontal y s3= vertical (figura
6.1a). Deliberadamente se omite s2 ya que, por orientarse paralelamente al rumbo del plano, no
influye en la ruptura. Por lo tanto, el análisis puede realizarse en dos dimensiones. Se elige un
tri·ngulo determinado por la intersección del plano P con los ejes coordenados x = horizontal y z =
vertical, el cual aparece aumentado de tamaño en la figura 6.1b. La posición del plano P queda
determinada por el ángulo a que forma la normal N al plano con el eje x y A es el ·área de la
hipotenusa.
Convenciones de los ángulos
Para determinar la posición del plano P , existen dos convenciones. La primera determina su
posición mediante el ángulo a que forma la normal al plano con la horizontal. La segunda
determina su posición por medio del ·ángulo q , que forma la dirección de s1 con el plano. Como los
dos·ángulos son complementarios (figura 6.3b), las ecuaciones de los círculos de Mohr son
igualmente válidas para ambos. Esto se expresa gráficamente en figura 6.3a con los ángulos dobles
en el círculo de Mohr, donde 2a + 2q = 180º. De este modo, las ecuaciones de los círculos de Mohr
también pueden expresarse en función del ángulo q :
EL CRITERIO DE NAVIER-COULOMB
Las condiciones que rigen la ruptura de cizalle de un material, a la vez que el ángulo que forman dos
sistemas de fallas conjugadas originados por el mismo campo de stress, pueden ser predichas por el
criterio de ruptura de Navier - Coulomb. Para que se produzca ruptura y deslizamiento a lo largo de
un plano de falla deben vencerse dos tipos de resistencias:
- Resistencia a la fricción.
- Resistencia cohesiva.
Fallas conjugadas
Analícese el caso de un par de fallas conjugadas que forman cada una un ángulo q con la dirección
del stress principal s1
Envolventes de Mohr
Teóricamente, las condiciones de ruptura están regidas por la recta de la ecuación de NavierCoulomb
y una serie de círculos de Mohr tangentes. El requisito de tangencia señala las condiciones
de stress (sn , t ) necesarias para iniciar la ruptura.Sin embargo, se comprueba en experimentos, que
si se toman los valores de sn y t correspondientes a distintos niveles de presión confinante s 3, la
función t = f (sn) no es lineal, sino que describe una curva denominada envolvente de Mohr (figura
6.11). Se aprecia que 2q crece desde un valor igual a 0º en P1 (condiciones de stress tensional, es
decir para sn =-T ), pasando por un valor de 69º en P2, hasta valores de 75º en P3, bajo stress
diferencial alto.



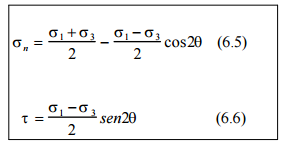






Comentarios
Publicar un comentario